5.25 Inch Disk Kickoff
I’ve started working on Apple II 5.25 inch disk emulation for Floppy Emu. It’s still early, and it’s progressing more slowly than I expected, but I think it’ll work. It will be great to have a new mode to emulate the zillions of 5.25 inch Apple II disks out there. I’ve been using the IIgs for my testing, but it should work on any Apple II series machine. No adapters needed either – just plug in the Emu board and go.
The first step was to convince the computer that there was even a 5.25 inch drive connected. That took more effort than I expected, because the 5.25 drive doesn’t have any way of directly telling the computer “I’m here”. After some trial and error, I discovered that the computer just blindly turns on the drive motor and starts reading from it. If it gets valid data or garbage data, either way it knows there’s a drive attached, but if it gets no data at all then it assumes no drive is present. I had assumed an empty drive would send no data, but some investigations with a logic analyzer proved that theory wrong. To make Floppy Emu be detected as an installed drive, I had to change the firmware to send a constant stream of sync bytes even when there’s no disk inserted.
Stepping the drive head to the correct track proved to be a major hassle. The Apple II directly controls a 4-phase stepper motor in the 5.25 disk drive, activating each coil in the correct sequence to move the stepper in or out. I modified the firmware to monitor these control signals, and simulate what would happen to a real stepper motor. This was more difficult than it might sound, because the control signals can be driven in various ways to produce half steps, full steps, or weird combinations of inputs that don’t do anything well-defined. Fortunately I think I’ve got it working now.
Speaking of the stepper controls, I hooked up my logic analyzer to the disk interface signals so I could see what was going on. For all the years I’ve been working on floppy emulation, I can’t believe I’ve never done this before! I normally rely on indirect methods of observation, from the computer or the Emu, and haven’t had a direct window onto the actual disk signals.
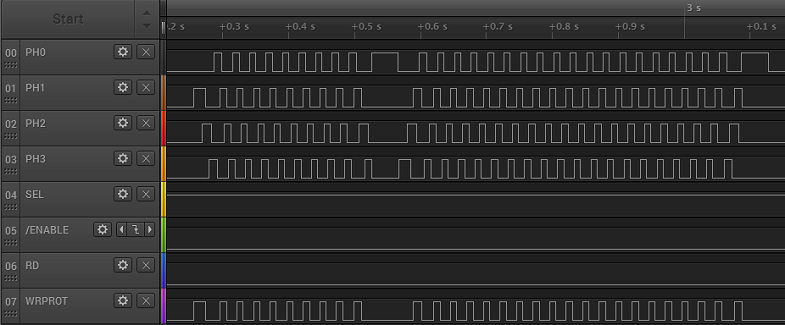
The waveform above shows the characteristic chukka-chukka-chukka of an Apple II 5.25 inch drive when the computer recalibrates the track position. During the first section, the phase lines are repeatedly activated one at a time in order, from lowest to highest, which moves the drive head outwards. Then there’s a pause, followed by a second section where the phase lines are activated from highest to lowest, which moves the drive head inward. Eventually the head hits a mechanical stop at track 0, making the familiar rattling sound of a 5.25 inch floppy drive.
For comparison, the waveform below shows what happens on the IIgs, just a brief moment after the power is turned on. Note that the time scale is much smaller, and the phase lines aren’t driven in sequence, but instead each one has an independent behavior. I believe this is the IIgs asking “Hello, are you a SmartPort hard disk? No? OK then.” I’ll find out more when I look further into SmartPort HD emulation.
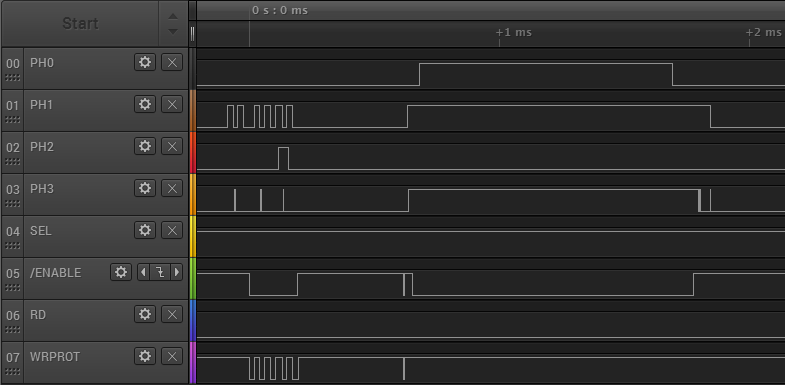
Copy II Plus, an Apple II disk copy program, has some very nice sector and track diagnostic tools built in. Using these I was able to verify that my track stepping logic is working. I was also able to capture a raw dump of an entire track, showing all the bytes straight off the disk (or the Emu), without any kind of post-processing to try to identify where the sectors are. This will be incredibly valuable as I start to work on actually sending the correct disk data.
In the image below, you can see that it’s already sort of working. This shows a Copy II Plus dump of track 0 of an emulated 5.25 inch disk from Floppy Emu. The data itself is actually from a Macintosh disk, with Macintosh style sector headers, so that part obviously isn’t right. But what’s encouraging is that the raw data is being received correctly by the Apple II – I circled the familiar D5 AA 96 that marks the start of a sector, and D5 AA AD that marks the start of the sector’s data payload.
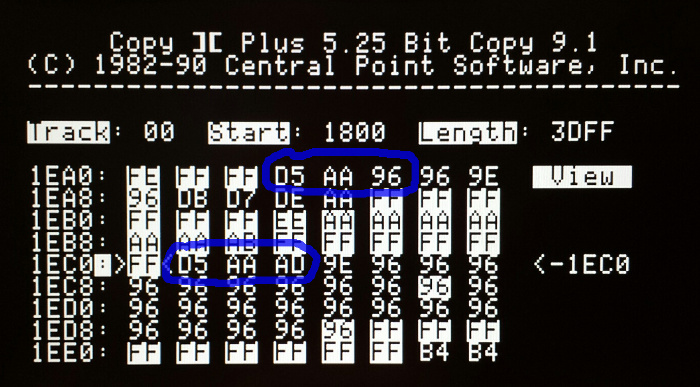
Unfortunately, some of the data is received incorrectly. The screenshot shows an example that mostly worked, but in many cases, parts of the sector are garbled. The data payload shown above should have contained hundreds of “96” bytes after the D5 AA AD, but it only has 23 of them before something goes wrong. Even the highlighted “FF” sync bytes before the data payload are wrong: some of them show “AA” and other incorrect values. Maybe the bit rate is slightly off? Bad voltage levels? Microcontroller interrupts messing with the bit timing? I’ll figure it out eventually.
Read 3 comments and join the conversation3 Comments so far
Leave a reply. For customer support issues, please use the Customer Support link instead of writing comments.


awesome progress! can’t wait to test it out.
Thanks! I’ve fixed the problem that was causing some data to be received incorrectly. It seems that the width of my “1” pulse was too narrow, and sometimes a 1 would be detected as a 0. So now I can emulate bytes on a 5.25 inch disk, and I just need to work on them being the correct bytes. That means changing the existing Mac-centric code to use a different sector header, and working with 256 byte sectors instead of 512 byte sectors, and a few other things. It may take a while to do the necessary replumbing work, but at least the theory is clear.
It works! I was able to boot an Apple II from an emulated 5.25 inch disk image of Oregon Trail. Tested on a IIgs with the built-in floppy connector, and also on a IIe with the 19-pin Disk 5.25 controller card, as well as on the IIe with an original Disk II card’s 20-pin connector. I still need to clean up a million loose ends and do a proper blog post showing off the new feature.